Important tips and formula to get through aptitude test

Various types of numbers in mathematics

A number is denoted by a group of digits, called numeral.

We have 1, 2, 3, 4, 5, 6, 7, 8 and 9 digits in use and written like one, two, three, four, five, six, seven, eight and nine.

Face value and place value:

Face value: The face value of a digit in a numeral is its own value, at whatever place it may be.  Ex. In the numeral 568, the face value of 8 is 8, the face value of 6 is 6 and face value of 5 is 5.

Place value: Place value can be calculated with below:

Place value of a unit digit = unit digit X 1

Place value of a tens digit = tens digit X 10

Place value of a hundred’s digit = hundred’s digit X 100

Hence in numeral 568,

Place value of 8 = 8*1=8

Place value of 6 = 6*10=60

Place value of 5 = 5*100=500

Natural numbers: 1, 2, 3…..9 all this counting numbers are called natural numbers.

Whole numbers: All counting numbers and 0 denote the set of whole numbers.

Ex. 0, 1, 2, 3………..9 are the whole numbers.

Integers: All counting numbers, zero and negative counting number denote the integers.

Ex. -3,-2, -1, 0, 1, 2, 3………9

Even numbers: 0, 2, 4, 6 and so on, which counting numbers are divisible by 2 is called even numbers.

Odd numbers: A counting numbers which are not divisible by 2 is called odd numbers. Ex.1, 3, 5……9.

Prime numbers: A counting number is called a prime number if it has exactly two factors, one is itself and other is 1.

“A counting number is called a prime number if it is divisible by two factors, namely itself and 1”.

Ex. 2, 3, 5, 7, 11, 13, 17… are few such prime numbers.

Divisibility Math Tricks to Learn the Facts (Divisibility)

More and more in my teaching career, I see that we often are able to enhance student learning in mathematics with tricks. There are many tricks to teach children divisibility in mathematics. Some tricks that I used to use in my classroom are listed here. If you know of some that I may have missed, drop into the forum and let everyone know. I'll add them to this list as I see them.

Dividing by 2

1. All even numbers are divisible by 2. E.g., all numbers ending in 0,2,4,6 or 8.

Dividing by 3

1. Add up all the digits in the number.
2. Find out what the sum is. If the sum is divisible by 3, so is the number
3. For example: 12123 (1+2+1+2+3=9) 9 is divisible by 3, therefore 12123 is too!

Dividing by 4

1. Are the last two digits in your number divisible by 4?
2. If so, the number is too!
3. For example: 358912 ends in 12 which is divisible by 4, thus so is 358912.

Dividing by 5

1. Numbers ending in a 5 or a 0 are always divisible by 5.

Dividing by 6

1. If the Number is divisible by 2 and 3 it is divisible by 6 also.

Dividing by 7 (2 Tests)

• Take the last digit in a number.
• Double and subtract the last digit in your number from the rest of the digits.
• Repeat the process for larger numbers.
• Example: 357 (Double the 7 to get 14. Subtract 14 from 35 to get 21 which is divisible by 7 and we can now say that 357 is divisible by 7.
  
  NEXT TEST
• Take the number and multiply each digit beginning on the right hand side (ones) by 1, 3, 2, 6, 4, 5. Repeat this sequence as necessary
• Add the products.
• If the sum is divisible by 7 - so is your number.
• Example: Is 2016 divisible by 7?
• 6(1) + 1(3) + 0(2) + 2(6) = 21
• 21 is divisible by 7 and we can now say that 2016 is also divisible by 7.

Dividing by 8

1. This one's not as easy, if the last 3 digits are divisible by 8, so is the entire number.
2. Example: 6008 - The last 3 digits are divisible by 8, therefore, so is 6008.

Dividing by 9

1. Almost the same rule and dividing by 3. Add up all the digits in the number.
2. Find out what the sum is. If the sum is divisible by 9, so is the number.
3. For example: 43785 (4+3+7+8+5=27) 27 is divisible by 9, therefore 43785 is too!

Dividing by 10

2. If the number ends in a 0, it is divisible by 10.
   
   
   Dividing By 11
   
   A number is divisible by 11 if the difference between the sum of it's digits at odd places
   and the sum of its digits at even places is either 0 or a number divisible by 11
   

Difference of cubes

Sum of cubes

 

Formula for (a+b)² and (a-b)²

 Formula for (a+b)³ and (a-b)³

Roots of Quadratic Equation

Formula

Consider this quadratic equation: 

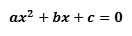
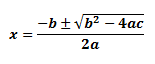
Where a, b and c are the leading coefficients.

The roots for this quadratic equation will be:

Arithmetic Progression

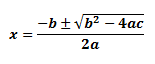
Arithmetic progression

Consider the following arithmetic progression:

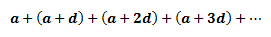
Where:

1. a is the initial term
2. d is the common difference

The n^th term

The n^th term, T_n of the arithmetic progression is:

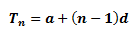
Sum of the first n term

The sum of the first n terms of the arithmetic progression is:

Geometric Progression

Geometric progression

Consider the following geometric progression:

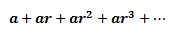
Where:

1. a is the scale factor
2. r is the common ratio

The n^th term

The n^th term, T_n of the geometric progression is:

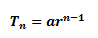
The sum of the first n terms

The sum of the first n terms, S_n is:

If -1 < r < 1, the sum to infinity, S_∞ is:

 

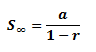
Average formula:

Let a₁,a₂,a₃,......,a_n be a set of numbers, average = (a₁ + a₂ + a₃,+......+ a_n)/n

Fractions formulas:

Converting a mixed number to an improper fraction:

Converting an improper fraction to a mixed number:

Formula for a proportion:

In a proportion, the product of the extremes (ad) equal the product of the means(bc),

Thus, ad = bc

Percent:

Percent to fraction: x% = x/100

Percentage formula: Rate/100 = Percentage/base

Rate: The percent.

Base: The amount you are taking the percent of.

Percentage: The answer obtained by multiplying the base by the rate

Consumer math formulas:

Discount = list price × discount rate

Sale price = list price − discount

Discount rate = discount ÷ list price

Sales tax = price of item × tax rate

Interest = principal × rate of interest × time

Tips = cost of meals × tip rate

Commission = cost of service × commission rate

Geometry formulas:

Perimeter:

Perimeter of a square: s + s + s + s

s:length of one side

Perimeter of a rectangle: l + w + l + w

l: length

w: width

Perimeter of a triangle: a + b + c

a, b, and c: lengths of the 3 sides

Area:

Area of a square: s × s

s: length of one side

Area of a rectangle: l × w

l: length

w: width

Area of a triangle: (b × h)/2

b: length of base

h: length of height

Area of a trapezoid: (b₁ + b₂) × h/2

b₁ and b₂: parallel sides or the bases

h: length of height

volume:

Volume of a cube: s × s × s

s: length of one side

Volume of a box: l × w × h

l: length

w: width

h: height

Volume of a sphere: (4/3) × pi × r³

pi: 3.14

r: radius of sphere

Volume of a triangular prism: area of triangle × Height = (1/2 base × height) × Height

base: length of the base of the triangle

height: height of the triangle

Height: height of the triangular prism

Volume of a cylinder:pi × r² × Height

pi: 3.14

r: radius of the circle of the base

Height: height of the cylinder

1. Speed, Time and Distance:
   
   

   Speed =		Distance		,	Time =		Distance		,	Distance = (Speed x Time).
   		Time					Speed

2. km/hr to m/sec conversion:
   
   

   x km/hr =		x x	5		m/sec.
   			18

3. m/sec to km/hr conversion:
   
   

   x m/sec =		x x	18		km/hr.
   			5

4. If the ratio of the speeds of A and B is a : b, then the ratio of the
   
   

   the times taken by then to cover the same distance is	1	:	1	or b : a.
   	a		b

5. Suppose a man covers a certain distance at x km/hr and an equal distance at y km/hr. Then,
   
   

   the average speed during the whole journey is		2xy		km/hr.
   		x + y

Time and Work Formula

If X can do a Piece of work in k days.
Than X one day’s work is =1/k

IF P is thrice as good a workman as Q then
Ratio of work done by P and Q= 3:1

Days* One day work= Total work done by person
One day work = Total work done by person/Days
 

Rule of Alligation
It is the rule that enables us to find the ratio in which two or more ingredients at the given price must be mixed to produce a mixture of a desired price.

Mean Price: The cost price of a unit quantity of the mixture is called mean price.


Rule of Alligation

If two quantities are mixed, then






Taking a simple example

In what ratio must rice at 9.30 /kg be mixed with rice at 10.80/kg so that the mixture be worth 10/kg?

C.P of cheaper=9.30
C.P of dearer=10.80
C.P of mean or mean price = 10.0

so putting the values in the formula


=

=8:7 Ans

Permutations

There are basically two types of permutation:

1. Repetition is Allowed: such as the lock above. It could be "333".
2. No Repetition: for example the first three people in a running race. You can't be first and second.

1. Permutations with Repetition

These are the easiest to calculate.

When you have n things to choose from ... you have n choices each time!

When choosing r of them, the permutations are:

n × n × ... (r times)

(In other words, there are n possibilities for the first choice, THEN there are n possibilites for the second choice, and so on, multplying each time.)

Which is easier to write down using an exponent of r:

n × n × ... (r times) = n^r

Example: in the lock above, there are 10 numbers to choose from (0,1,..9) and you choose 3 of them:

10 × 10 × ... (3 times) = 10³ = 1,000 permutations

So, the formula is simply:

nr

where n is the number of things to choose from, and you choose r of them (Repetition allowed, order matters)

2. Permutations without Repetition

In this case, you have to reduce the number of available choices each time.

For example, what order could 16 pool balls be in? After choosing, say, number "14" you can't choose it again.

So, your first choice would have 16 possibilites, and your next choice would then have 15 possibilities, then 14, 13, etc. And the total permutations would be:

16 × 15 × 14 × 13 × ... = 20,922,789,888,000

But maybe you don't want to choose them all, just 3 of them, so that would be only:

16 × 15 × 14 = 3,360

In other words, there are 3,360 different ways that 3 pool balls could be selected out of 16 balls.

But how do we write that mathematically? Answer: we use the "factorial function"

	The factorial function (symbol: !) just means to multiply a series of descending natural numbers. Examples: 4! = 4 × 3 × 2 × 1 = 24 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5,040 1! = 1
Note: it is generally agreed that 0! = 1. It may seem funny that multiplying no numbers together gets you 1, but it helps simplify a lot of equations.

So, if you wanted to select all of the billiard balls the permutations would be:

16! = 20,922,789,888,000

But if you wanted to select just 3, then you have to stop the multiplying after 14. How do you do that? There is a neat trick ... you divide by 13! ...

16 × 15 × 14 × 13 × 12 ...		= 16 × 15 × 14 = 3,360
13 × 12 ...

Do you see? 16! / 13! = 16 × 15 × 14

The formula is written:

where n is the number of things to choose from, and you choose r of them (No repetition, order matters)

Examples:

Our "order of 3 out of 16 pool balls example" would be:

16!	=	16!	=	20,922,789,888,000	= 3,360
(16-3)!		13!		6,227,020,800

(which is just the same as: 16 × 15 × 14 = 3,360)

How many ways can first and second place be awarded to 10 people?

10!	=	10!	=	3,628,800	= 90
(10-2)!		8!		40,320

(which is just the same as: 10 × 9 = 90)

Notation

Instead of writing the whole formula, people use different notations such as these:

Example: P(10,2) = 90

Combinations

There are also two types of combinations (remember the order does not matter now):

1. Repetition is Allowed: such as coins in your pocket (5,5,5,10,10)
2. No Repetition: such as lottery numbers (2,14,15,27,30,33)

1. Combinations with Repetition

Actually, these are the hardest to explain, so I will come back to this later.

2. Combinations without Repetition

This is how lotteries work. The numbers are drawn one at a time, and if you have the lucky numbers (no matter what order) you win!

The easiest way to explain it is to:

• assume that the order does matter (ie permutations),
• then alter it so the order does not matter.

Going back to our pool ball example, let us say that you just want to know which 3 pool balls were chosen, not the order.

We already know that 3 out of 16 gave us 3,360 permutations.

But many of those will be the same to us now, because we don't care what order!

For example, let us say balls 1, 2 and 3 were chosen. These are the possibilites:

Order does matter	Order doesn't matter
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1	1 2 3

So, the permutations will have 6 times as many possibilites.

In fact there is an easy way to work out how many ways "1 2 3" could be placed in order, and we have already talked about it. The answer is:

3! = 3 × 2 × 1 = 6

(Another example: 4 things can be placed in 4! = 4 × 3 × 2 × 1 = 24 different ways, try it for yourself!)

So, all we need to do is adjust our permutations formula to reduce it by how many ways the objects could be in order (because we aren't interested in the order any more):

That formula is so important it is often just written in big parentheses like this:

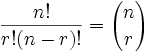where n is the number of things to choose from, and you choose r of them (No repetition, order doesn't matter)

It is often called "n choose r" (such as "16 choose 3")
And is also known as the "Binomial Coefficient"

Notation

As well as the "big parentheses", people also use these notations: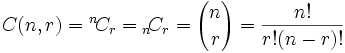

Example

So, our pool ball example (now without order) is:

16!	=	16!	=	20,922,789,888,000	= 560
3!(16-3)!		3!×13!		6×6,227,020,800

Or you could do it this way:

16×15×14	=	3360	= 560
3×2×1		6

So remember, do the permutation, then reduce by a further "r!"

... or better still ...

Remember the Formula!

It is interesting to also note how this formula is nice and symmetrical:

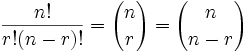
In other words choosing 3 balls out of 16, or choosing 13 balls out of 16 have the same number of combinations.

16!	=	16!	=	16!	= 560
3!(16-3)!		13!(16-13)!		3!×13!

Pascal's Triangle

You can also use Pascal's Triangle to find the values. Go down to row "n" (the top row is 0), and then along "r" places and the value there is your answer. Here is an extract showing row 16:

1    14    91    364  ...

1    15    105   455   1365  ...

1    16   120   560   1820  4368  ...

1. Combinations with Repetition

OK, now we can tackle this one ...

Let us say there are five flavors of icecream: banana, chocolate, lemon, strawberry and vanilla. You can have three scoops. How many variations will there be? Let's use letters for the flavors: {b, c, l, s, v}. Example selections would be {c, c, c} (3 scoops of chocolate) {b, l, v} (one each of banana, lemon and vanilla) {b, v, v} (one of banana, two of vanilla)

(And just to be clear: There are n=5 things to choose from, and you choose r=3 of them.
Order does not matter, and you can repeat!)

Now, I can't describe directly to you how to calculate this, but I can show you a special technique that lets you work it out.

	Think about the ice cream being in boxes, you could say "move past the first box, then take 3 scoops, then move along 3 more boxes to the end" and you will have 3 scoops of chocolate!
	So, it is like you are ordering a robot to get your ice cream, but it doesn't change anything, you still get what you want.

Now you could write this down as (arrow means move, circle means scoop).

In fact the three examples above would be written like this:

{c, c, c} (3 scoops of chocolate):
{b, l, v} (one each of banana, lemon and vanilla):
{b, v, v} (one of banana, two of vanilla):

OK, so instead of worrying about different flavors, we have a simpler problem to solve: "how many different ways can you arrange arrows and circles"

Notice that there are always 3 circles (3 scoops of ice cream) and 4 arrows (you need to move 4 times to go from the 1st to 5th container).

So (being general here) there are r + (n-1) positions, and we want to choose r of them to have circles.

This is like saying "we have r + (n-1) pool balls and want to choose r of them". In other words it is now like the pool balls problem, but with slightly changed numbers. And you would write it like this:

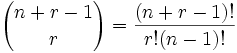where n is the number of things to choose from, and you choose r of them (Repetition allowed, order doesn't matter)

Interestingly, we could have looked at the arrows instead of the circles, and we would have then been saying "we have r + (n-1) positions and want to choose (n-1) of them to have arrows", and the answer would be the same ...

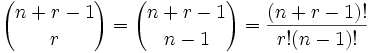
So, what about our example, what is the answer?

(5+3-1)! = 7! = 5040 = 35 3!(5-1)! 3!×4! 6×24 0 ≤ p(A) ≤ 1 p(S) = 1 Probability Formula Addition Rule If A B ≠ . p(A B) = p(A) + p(B) − p(A B) p(A B C) = p(A) + p(B) + p(C) − p(A B) − p(A C) − p(B C) + p(A B C) Multiplication Rule Independent Events p(A B) = p(A) · p(B) Dependent Events p(A B) = p(A) · p(B|A) Conditional Probability Independent Events p(A|B) = p(A) Dependent Events p(A|B) ≠ p(A) Law of Total Probability p(B) = p(A1) · p(B|A1) + p(A2) · p(B|A2 ) + ... + p(An) · p(B|An ) Bayes' Theorem Expected Value Variance of a Discrete Random Variable Standard Deviation of a Discrete Random Variable Binomial Distribution Normal Approximation to the Binomial